微前端qiankun调研

背景

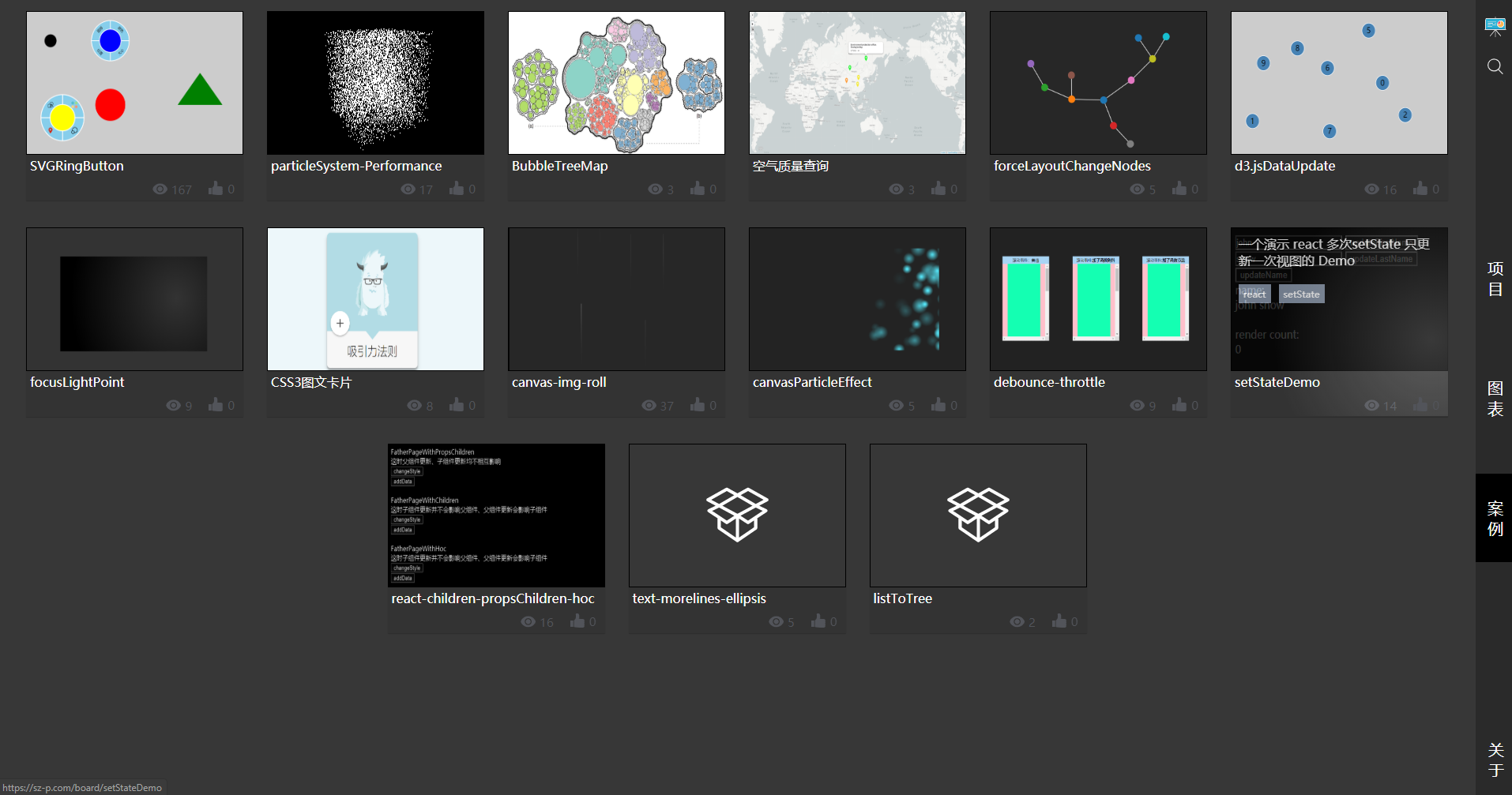
有一个程序集成展示站点。如上图所示，整体架构为一个主程序壳子即上图所示的站点，一些案例子程序即上图中的各个展示案例。

图表推荐调研

背景 & 目的

图表选择困难，拿到一份数据是应该用饼图还是用柱图去展示？工程视往往有工程视的判断、设计师有设计师的考量，同时产品和客户的意愿可能又不相同。到底这个数据最适合采用哪种图表去展示？以前我们普遍的采用朴素经验主义，即以前用的啥，我们现在还用啥、别的用的啥我们就用啥。这种方式既不科学、也没有说服力。所以我们需要去维护一套知识库，界合经验和分析去判断哪些那些类的数据更适合用哪种图表展示。本质上是解决一个数据到图表种类的映射关系。

前言

本文主要基于。即阿里的autoChart去分析他们所采用的解决方案。调研对于该问题，他们的解决方案是否可行，优点以及不足。

简介

AVA Visual Analytics) 是为了更简便的可视分析而生的技术框架。 其名称中的第一个 A 具有多重涵义：它说明了这是一个出自阿里巴巴集团（Alibaba）技术框架，其目标是成为一个自动化（Automated）、智能驱动（AI driven）、支持增强分析（Augmented）的可视分析解决方案。（引用自 ava Readme）

1. 已知两圆的圆心和半径，第三圆的半径，且三圆两两相切，求第三圆圆心坐标。设圆1圆心,半径为 $$ x_1,y_1,r_1 $$ , 圆2 $$ x_2,y_2,r_2 $$ 。圆3 $$ x_3,y_3,r_3 $$ 即可得

   1. 公式1.1 $$ (x_3-x_1)^2 + (y_3-y_1)^2 = (r_3+r_1)^2 = d31 $$

   2. $$ (x_3-x_2)^2 + (y_3-y_2)^2 = (r_3+r_2)^2 = d32 $$

   3. $$ (x_2-x_1)^2 + (y_2-y_1)^2 = (r_1+r_2)^2 = d21 $$

   根据1、2、3式即得：

   1. $$ x = (d21+d32-d31)/(2*d21) $$

   2. $$ y = \sqrt{d32/d21 - x^2} $$

海伦公式

$$ S = \sqrt{p(p-a)(p-b)(p-c)} $$

假设在平面内，有一个三角形，边长分别为a、b、c，三角形的面积S可由以下海伦公式求得，其中p为半周长（周长的一半）$p=\frac{a+b+c}{2}$

凸包算法

背景

凸包算法其实是一个挺常用的算法，例如在这道题(812.最大三角形面积)中，常规的解决方案就是写一个时间复杂度O(N^3)的暴力算法去枚举所有可能出现的三角形，再利用海伦公式去求得三角形面积。不妨我们大胆假设，在一堆点的集合中，其中面积最大的三角形的顶点，必然位于这些点的凸包上。论证我们先跳过，直接用结果去验证假设是否成立(经验证，假设是成立的)

简介

凸包算法有很多种，例如

1. Graham扫描法 nlogn
2. Jarvis步进法 nH (H为凸包上的点 最差情况会退化成 n^2)
3. 分治法 nlogn
4. 穷举法 n^3 (两点确定一条直线，如果剩余的其它点都在这条直线的同一侧，则这两个点是凸包上的点，否则就不是)
5. Melkman算法 (基于双向链表来做的，具体没看懂)

这里详细介绍常规的 Graham扫描法,Graham扫描法时间复杂度优于Jarvis步进法，理解起来稍微比之困难一些，但影响不大。

WSL初探

特色

1. ip共享 win下启动的web服务wsl可直接访问。
2. 资源共享 win下 及 wsl下访问资源占用情况均为物理机的资源占用情况。
3. 支持docker

样式文件的动态引用

背景

要实现一个主题切换功能，通常的解决方案是替换css文件，由此就引出了样式文件的动态引用。样式文件的动态引用普遍有两种方式。

泛洪算法 Flood Fill

简介

泛洪算法——Flood Fill，（也称为种子填充——Seed Fill）是一种算法，用于确定连接到多维数组中给定节点的区域。 它被用在油漆程序的“桶”填充工具中，用于填充具有不同颜色的连接的，颜色相似的区域，并且在诸如围棋（Go）和扫雷（Minesweeper）之类的游戏中用于确定哪些块被清除。泛洪算法的基本原理就是从一个像素点出发，以此向周边相同或相似的像素点扩充着色，直到周边无相同颜色的区块或到图像边界为止。

泛洪填充算法采用三个参数：起始节点（start node），目标颜色（target color）和替换颜色（replacement color）。 该算法查找阵列中通过目标颜色的路径连接到起始节点的所有节点，并将它们更改为替换颜色。 可以通过多种方式构建泛洪填充算法，但它们都明确地或隐式地使用队列或堆栈数据结构。

机器学习算法学习思路

机器学习的算法相对都比较抽象，需要一定的数学功底，这里简单的列一下机器学习算法学习思路，这个应该按照什么个流程去学习收获最快。

流程: 目的→输入输出→思想→流程→代码→原理→数学依据。

大白话版：干啥的→干了啥→怎么干→为什么可以这么干。

大致可以按照上述流程去执行。

首先了解这个算法的目的，解决他是干啥的这个问题，再去了解它的输入输出，这其实是解决了它干了啥这个问题。到这里算是解决了这个算法怎么用的问题，做到了能用。

了解完它的输入输出之后可以去了解这个算法的思想，执行过程、代码。这部分可以总结成怎么干。到这部分其实算是对算法有了一个具体认知。知道数据集和各个参数具体对结果造成了那些影响。算是做到会用。

之后可以尝试了解算法的原理，看懂数学公式算是了解原理，理解推倒过程算是了解数据依据。这一大步是在解决为什么可以这么干的问题。这一步走完算是掌握

K-Means

简介

K-Means算法是无监督的聚类算法，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。

输入输出

K-Means是根据样本之间距离的大小来判断是否属于同一个簇的，所以样本必须能够计算距离，即必须包含坐标信息。将样本集划分为K个簇，即参数为K。

输入依赖： 包含坐标信息的样本集、要划分为K个簇的K值，输出：给样本集标注每个样本分别属于哪一个K簇

思想

K-Means算法的思想很简单，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。